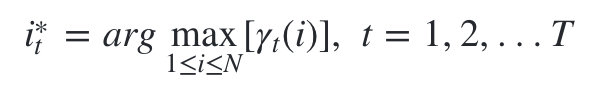19.5 维特比算法解码隐藏状态序列
学习目标
- 知道维特比算法解码隐藏状态序列
在本篇我们会讨论维特比算法解码隐藏状态序列,即给定模型和观测序列,求给定观测序列条件下,最可能出现的对应的隐藏状态序列。
HMM模型的解码问题最常用的算法是维特比算法,当然也有其他的算法可以求解这个问题。
同时维特比算法是一个通用的求序列最短路径的动态规划算法,也可以用于很多其他问题。
1 HMM最可能隐藏状态序列求解概述
HMM模型的解码问题即:
- 给定模型 λ=(A,B,Π) 和观测序列
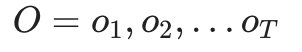 ,求给定观测序列O条件下,最可能出现的对应的状态序列
,求给定观测序列O条件下,最可能出现的对应的状态序列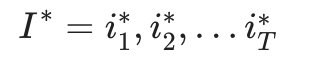 ,即
,即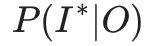 的最大化。
的最大化。
一个可能的近似解法是求出观测序列O在每个时刻t最可能的隐藏状态 然后得到一个近似的隐藏状态序列
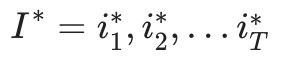 。要这样近似求解不难,利用前向后向算法评估观察序列概率的定义:
。要这样近似求解不难,利用前向后向算法评估观察序列概率的定义:
在给定模型λ和观测序列O时,在时刻t处于状态q_i的概率是
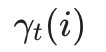
,这个概率可以通过HMM的前向算法与后向算法计算。这样我们有:
近似算法很简单,但是却不能保证预测的状态序列整体是最可能的状态序列,因为预测的状态序列中某些相邻的隐藏状态可能存在转移概率为0的情况。
而维特比算法可以将HMM的状态序列作为一个整体来考虑,避免近似算法的问题,下面我们来看看维特比算法进行HMM解码的方法。
2 维特比算法概述
维特比算法是一个通用的解码算法,是基于动态规划的求序列最短路径的方法。
既然是动态规划算法,那么就需要找到合适的局部状态,以及局部状态的递推公式。在HMM中,维特比算法定义了两个局部状态用于递推。
- 第一个局部状态是在时刻t隐藏状态为 i 所有可能的状态转移路径
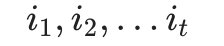 中的概率最大值。
中的概率最大值。
- 记为
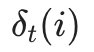 :
:
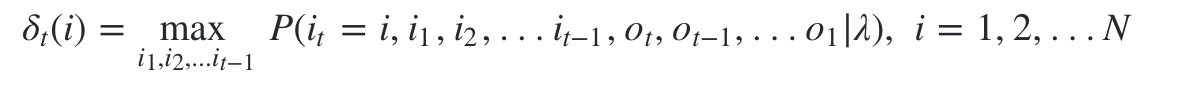
由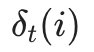 的定义可以得到
的定义可以得到 的递推表达式:
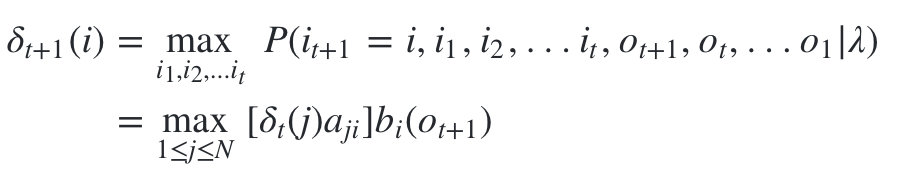
- 第二个局部状态由第一个局部状态递推得到。
- 我们定义在时刻t隐藏状态为i的所有单个状态转移路径
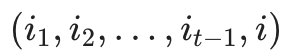 中概率最大的转移路径中第t-1个节点的隐藏状态为:
中概率最大的转移路径中第t-1个节点的隐藏状态为: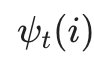
- 其递推表达式可以表示为:
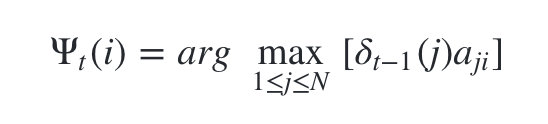
有了这两个局部状态,我们就可以从时刻0一直递推到时刻T,然后利用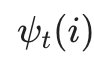 记录的前一个最可能的状态节点回溯,直到找到最优的隐藏状态序列。
记录的前一个最可能的状态节点回溯,直到找到最优的隐藏状态序列。
3 维特比算法流程总结
现在我们来总结下维特比算法的流程:
- 输入:HMM模型 λ=(A,B,Π),观测序列
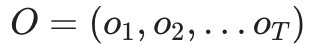
- 输出:最有可能的隐藏状态序列
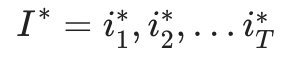
流程如下:
- 1)初始化局部状态:
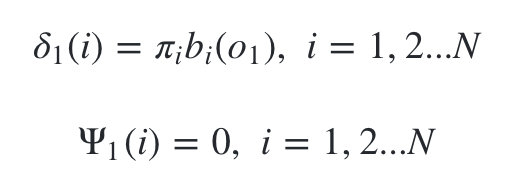
- 进行动态规划递推时刻 t=2,3,...T 时刻的局部状态:
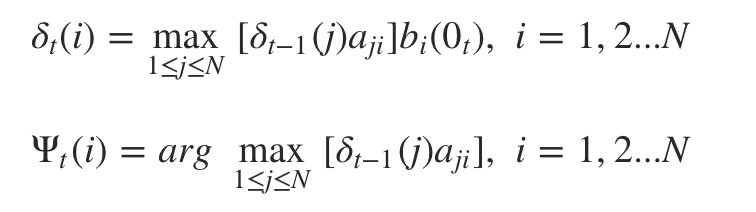
- 计算时刻T最大的
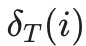 ,即为最可能隐藏状态序列出现的概率。计算时刻T最大的
,即为最可能隐藏状态序列出现的概率。计算时刻T最大的 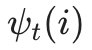 ,即为时刻T最可能的隐藏状态。
,即为时刻T最可能的隐藏状态。
- 计算时刻T最大的
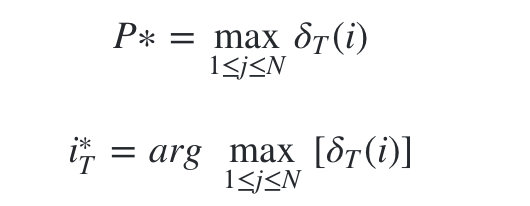
- 利用局部状态
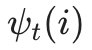 开始回溯。对于 t=T-1,T-2,...,1
开始回溯。对于 t=T-1,T-2,...,1
- 利用局部状态
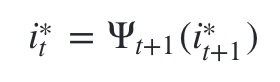
最终得到最有可能的隐藏状态序列: 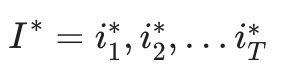
4 HMM维特比算法求解实例
下面我们仍然用盒子与球的例子来看看HMM维特比算法求解。 我们的观察集合是:

我们的状态集合是:

而观察序列和状态序列的长度为3.
初始状态分布为:
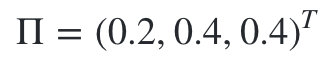
状态转移概率分布矩阵为:

观测状态概率矩阵为:
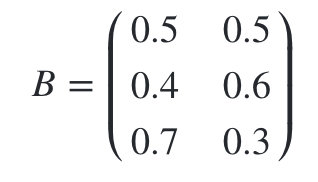
球的颜色的观测序列:

按照我们前面的维特比算法,首先需要得到三个隐藏状态在时刻1时对应的各自两个局部状态,此时观测状态为1:
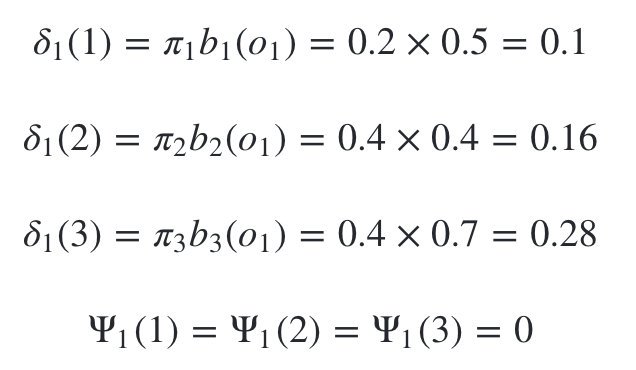
现在开始递推三个隐藏状态在时刻2时对应的各自两个局部状态,此时观测状态为2:
$$ \delta_2(1) = \max_{1\leq j \leq 3}[\delta_1(j)a_{j1}]b_1(o_2) = \max_{1\leq j \leq 3}[0.1 \times 0.5, 0.16 \times 0.3, 0.28\times 0.2] \times 0.5 = 0.028 $$
- $$ \Psi_2(1)=3 $$
$$ \delta_2(2) = \max_{1\leq j \leq 3}[\delta_1(j)a_{j2}]b_2(o_2) = \max_{1\leq j \leq 3}[0.1 \times 0.2, 0.16 \times 0.5, 0.28\times 0.3] \times 0.6 = 0.0504 $$
- $$ \Psi_2(2)=3 $$
$$ \delta_2(3) = \max_{1\leq j \leq 3}[\delta_1(j)a_{j3}]b_3(o_2) = \max_{1\leq j \leq 3}[0.1 \times 0.3, 0.16 \times 0.2, 0.28\times 0.5] \times 0.3 = 0.042 $$
- $$ \Psi_2(3)=3 $$
继续递推三个隐藏状态在时刻3时对应的各自两个局部状态,此时观测状态为1:
$$ \delta_3(1) = \max_{1\leq j \leq 3}[\delta_2(j)a_{j1}]b_1(o_3) = \max_{1\leq j \leq 3}[0.028 \times 0.5, 0.0504 \times 0.3, 0.042\times 0.2] \times 0.5 = 0.00756 $$
- $$ \Psi_3(1)=2 $$
$$ \delta_3(2) = \max_{1\leq j \leq 3}[\delta_2(j)a_{j2}]b_2(o_3) = \max_{1\leq j \leq 3}[0.028 \times 0.2, 0.0504\times 0.5, 0.042\times 0.3] \times 0.4 = 0.01008 $$
- $$ \Psi_3(2)=2 $$
$$ \delta_3(3) = \max_{1\leq j \leq 3}[\delta_2(j)a_{j3}]b_3(o_3) = \max_{1\leq j \leq 3}[0.028 \times 0.3, 0.0504 \times 0.2, 0.042\times 0.5] \times 0.7 = 0.0147 $$
- $$ \Psi_3(3)=3 $$

5 小结
- 维特比算法流程总结:
- 输入:HMM模型 λ=(A,B,Π),观测序列
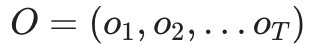
- 输出:最有可能的隐藏状态序列
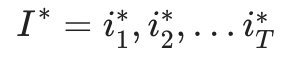
- 输入:HMM模型 λ=(A,B,Π),观测序列
流程如下:
- 1)初始化局部状态:
<img src="https://tva1.sinaimg.cn/large/006tNbRwgy1g9stj3olhyj30ea058q34.jpg" alt="image-20191211153308449" style="zoom:50%;" />
- 2) 进行动态规划递推时刻 t=2,3,...T 时刻的局部状态:
<img src="https://tva1.sinaimg.cn/large/006tNbRwgy1g9stjsyu1gj30l005wjs0.jpg" alt="image-20191211153349430" style="zoom:50%;" />
- 3) 计算时刻T最大的<img src="https://tva1.sinaimg.cn/large/007S8ZIlly1gfn24eyk3nj302e01amwy.jpg" alt="image-20200610115901486" style="zoom:50%;" />,即为最可能隐藏状态序列出现的概率。计算时刻T最大的 <img src="https://tva1.sinaimg.cn/large/007S8ZIlly1gfn24uawzyj302k01eq2q.jpg" alt="image-20200610115925436" style="zoom:50%;" />,即为时刻T最可能的隐藏状态。
<img src="https://tva1.sinaimg.cn/large/006tNbRwgy1g9stk7cwk8j30eq05qmxf.jpg" alt="image-20191211153412145" style="zoom:50%;" />
- 4) 利用局部状态<img src="https://tva1.sinaimg.cn/large/007S8ZIlly1gfn256ihlaj302k01eq2q.jpg" alt="image-20200610115945012" style="zoom:50%;" />开始回溯。对于 t=T-1,T-2,...,1
<img src="https://tva1.sinaimg.cn/large/006tNbRwgy1g9stm7kry6j307s02a0sl.jpg" alt="image-20191211153607900" style="zoom:50%;" />
最终得到最有可能的隐藏状态序列: <img src="https://tva1.sinaimg.cn/large/007S8ZIlly1gfn2g9fiwzj308801wq2s